從經驗中學習 - 直觀理解貝氏定理及其應用

貝氏定理（Bayes' theorem）是機率論中，一個概念簡單卻非常強大的定理。有了機率論的存在，人們才能理性且合理地評估未知事物發生的可能性（例：今天的下雨機率有多少？我中樂透的可能性有多高？），並透過貝氏定理搭配經驗法則來不斷地改善目前的認知，協助我們做更好的決策。

英國數學家哈羅德·傑弗里斯甚至說過：

貝氏定理之於機率論，就像是畢氏定理之於幾何學。

因為其簡單且強大的特性，被廣泛應用在醫療診斷以及機器學習等領域。網路並不缺貝氏定理的教學文章，但多數以機率公式出發，不夠直觀（至少以我個人來說），就算理解了也不易內化成自己的知識。

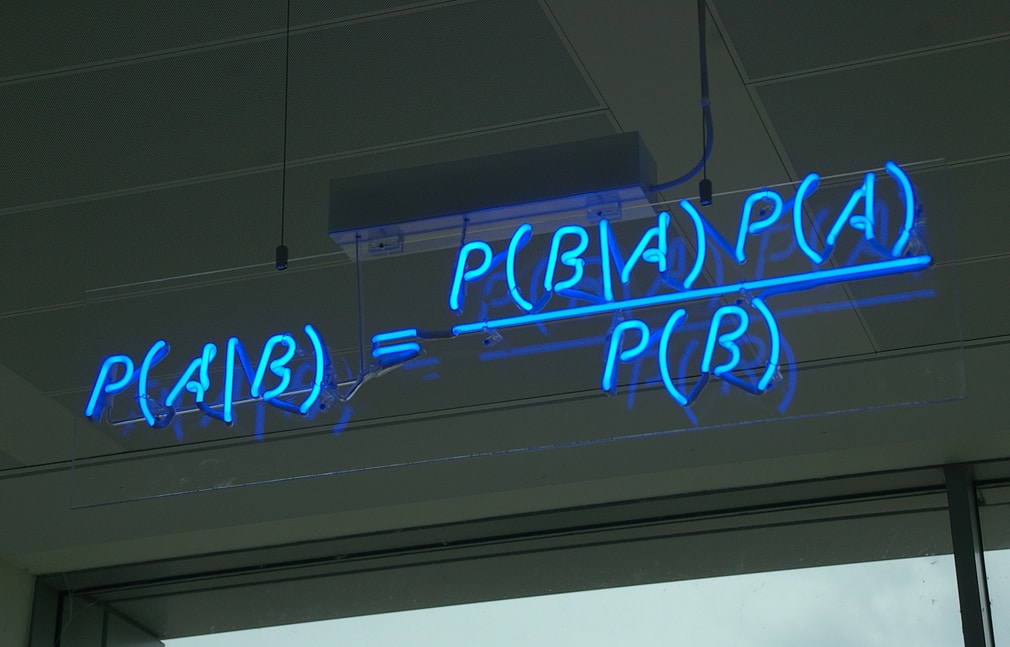
因此這篇將利用生活上我們（或人工智慧）常需要考慮的事情當作引子，如：

• 今天的下雨機率是多少？
• 這封 email 是垃圾郵件的可能性有多高？
• 醫生說我得癌症了，這可靠度有多高？（好吧，或許這沒那麼常發生）

來直觀地了解貝氏定理是怎麼被應用在各式各樣的地方。我們甚至可以效仿貝氏定理的精神，讓自己能更理性地評估未知並從經驗中學習。

廢話不多說，讓我們開始吧！

今天會下雨嗎？¶

在實際說明貝氏定理的公式把你嚇跑之前，讓我們先做個簡單的假想實驗來說明貝氏定理的精神。

假設大雄一早準備出門跟靜香見面，正在考慮要不要帶傘出門。

起床的時候他想：

「這地區不太會下雨，不需要帶傘吧！」

往窗外一看，大雄眉頭一皺，發現烏雲密佈。

「痾有烏雲，感覺下雨機率上升了，但好懶得帶傘 .. 先吃完早餐再說吧。」

走到廚房，發現餐桌上一大堆螞蟻在開趴。

「依據老媽的智慧，螞蟻往屋內跑代表下雨機率又提升了。真的不得不帶傘了嗎 .. 不不不！我不要帶好麻煩！」

想著想著，這時候靜香打電話過來了：

「胖虎說他也要去喔！」「蛤你說什麼！？」

胖虎是有名的雨男，每次跟他出遊都會下雨。依照這個經驗以及前面看到的幾個現象，最後大雄放棄掙扎，帶著雨傘出門了。

在上面的例子中，大雄觀察到三個現象：

• 烏雲密佈
• 螞蟻開趴
• 胖虎出沒

依據他過往的經驗，這些現象都會使得降雨的機率提升，讓他逐漸改變剛起床的時候「今天不太會下雨」的想法，最後決定帶傘出門。

這個決策的轉變過程，其實就是貝氏定理的精神：

針對眼前發生的現象以及獲得的新資訊，搭配過往經驗，來修正一開始的想法。

實際上，大雄已經在腦海中進行了多次貝氏定理的運算而不自知（我家大雄哪有那麼聰明）。現在讓我們用比較數學的方式來重現大雄腦海中的運算。

讓我們帶點數字進去¶

在了解貝氏定理的目的以後，讓我們以發生比（odds）的方式來闡述定理。發生比很簡單，就只是列出兩個（或以上）的事件分別（可能）發生的次數。

使用發生比的好處是可以很容易地比較不同事件發生的相對次數。後面會看到，我們也能把發生比轉成機率。

假設依據過往氣象紀錄，大雄住的地區一年 365 天中有 270 天放晴，下雨的天數為 365 - 270 = 95 天。則下雨的發生比為：

雨天數：晴天數 = 95：270

你可以把發生比想像成是一種相對關係，上面這個發生比代表，在大雄所住的地區，每觀測到 95 個雨天的日子，我們同時會觀測到 270 個晴天。晴天約是雨天的三倍之多（270 / 95）。

轉換成機率來看的話，就是把雨天的天數，去除以所有天數：

95 / (95 + 270) = 0.26 = 26%

一年也就只有 26% 的降雨機會，這也是為何大雄一開始在還沒觀察到新現象（烏雲、螞蟻及胖虎）的時候，合理認為今天「應該」不會下雨的原因。

我們再繼續假設，依據大雄的過往經驗，他發現：

• 雨天時，早上烏雲密佈的頻率是晴天時出現烏雲的 9 倍

這個 9 倍是怎麼來的呢？

這其實是所謂的概度比（likelihood ratio）。分別計算雨天及晴天發生的情況下，出現「烏雲密佈」現象的機率以後，再將兩者相除：

雨天時烏雲密佈的機率 = P(烏雲|雨天）
-------------------------------
晴天時烏雲密佈的機率 = P(烏雲|晴天）

這兩個機率又被稱為條件機率（conditional probability）。一般 P(A|B) 代表在事件 B 發生的情況下，事件 A 發生的機率。

假設平均來看，在 10 個雨天裡頭，早上烏雲密佈的天數為 9 天（也就是說平均有 1 天的雨天是早上沒有烏雲密佈的），則我們可以說，「給定雨天的條件下，烏雲密佈」的機率是：

P(烏雲|雨天） = 9 / 10

另外在 10 個晴天裡頭，早上烏雲密佈的天數平均為 1 天（也就是說早上雖然烏雲密佈，但最後並沒有下雨的天數），則「給定晴天的條件下，烏雲密佈」的機率是：

P(烏雲|晴天） = 1 / 10

則烏雲密佈的概度比即為：

P(烏雲|雨天）    9 / 10
-----------  = --------- = 9
P(烏雲|晴天）    1 / 10

雖然「概度比」一詞很饒舌，但它就是一個比例，也就是「幾分之幾」的概念。 9 就是「一分之九」＝ 9 倍，而因為分母是「晴天」，你可以解讀這個 9 為

• 「在烏雲密佈發生的情況下，每觀測到 1 個晴天，就會同時觀測到 9 個雨天」。

也可以像是大雄觀察到的：

• 「雨天時，早上烏雲密佈的頻率是晴天時出現烏雲的 9 倍」。

貝氏定理初顯鋒芒¶

所以有了這個倍數可以做什麼？直覺及經驗告訴我們，在觀測到烏雲密佈的前提下，下雨機率理論上會有所提升。

換句話說，在烏雲密佈，且觀測到的晴天數不變的情況下，觀測到的雨天數應該要有所上升，這樣下雨的天數在所有天數裡頭的比例才會上升。

而其上升的倍數就是前面的概度比（ 9 倍）。因此在烏雲密佈發生的情況下，新的下雨發生比（odds）可以寫成：

新雨天數：晴天數 = 原雨天數 * 概度比：晴天數
　　　　　　　　 =   95   *   9   ： 270
　　　　　　　　 =       855      ： 270

新的下雨發生比是我們利用觀測到的現象重新計算的，因此一般稱為「事後發生比」（posterior odds）；而一開始的發生比則被稱為「事前發生比」（prior odds）。

事後發生比告訴我們，在烏雲密佈的情況下，每觀測 855 個雨天，就會同時觀測到 270 個晴天。跟事前發生比相反，現在雨天數反而超過晴天的三倍（855 /　270）。

要計算新的下雨機率，我們一樣把雨天數去除以所有天數：

855 / (855 + 270) = 0.76 = 76%

跟一開始的 26% 相比，在觀測到烏雲密佈這個現象以後，下雨的機率足足上升了 50 個百分點，現在我們有更充分的理由請大雄帶把傘了。

實際上，透過上面的計算，我們已經套用貝氏定理的公式了（發生比版本）：

事後發生比 = 概度比 * 事前發生比

如同大雄的例子，一般應用貝氏定理的情境如下：

1. 對一件未知事物有初步的猜測（事前發生比）
2. 觀測到跟該事物相關的現象
3. 利用先前跟該現象有關的經驗計算出概度比
4. 利用概度比修正該猜測，得到修正後結果（事後發生比）
5. 重新評估、做決策
6. 又觀察到新現象，重複步驟 3 到 5

透過貝氏定理，我們可以很快速地利用過去的經驗改善自己的想法，並產生更好的決策。

大雄不死心：單純貝式¶

雖然觀察到了烏雲密佈，且利用過往經驗修正下雨的機率到了 76%，懶惰的大雄一開始還是不想帶傘出去。但為何最後還是帶傘出門了呢？那是因為除了烏雲密佈以外，他還觀察到了其他兩個影響下雨機率的現象：

• 螞蟻開趴
• 胖虎出沒

貝氏定理本身雖然強大，但其中一個使它被廣泛利用的是單純貝式（Naive Bayes）的概念：假設不同現象之間出現的機率為獨立)。

設成獨立有什麼好處？事情變得很簡單，我們不用考慮現象 A 跟現象 B 之間的關聯性，能針對每個現象，分別去計算概度比，修正從「前面」的現象得到的結果，持續改善我們的認知。也就是上一節提到的貝氏定理的應用步驟 6。

如法炮製，讓我們假設大雄針對其他兩個現象的經驗是：

• 雨天時，螞蟻出現在室內的天數是晴天的 2 倍
• 雨天時，胖虎出遊的次數是晴天的 3 倍

讓我們再次套用貝氏定理，但這次不是套用在一開始什麼都不知道的事前發生比：

雨天數：晴天數 = 95：270

而是在觀察到烏雲密佈後的事後發生比：

烏雲密佈下的雨天數：晴天數 = 855：270

首先，讓我們套用跟螞蟻相關的經驗：

• 雨天時螞蟻出現在室內的天數是晴天的 2 倍

概度比已經算好，所以依照貝氏定理的公式：

事後發生比 = 概度比 * 事前發生比

新的（螞蟻）事後發生比為：

新雨天數：晴天數 = 原雨天數 * 概度比：晴天數
　　　　　　　　 =   855  *   2   ： 270
　　　　　　　　 =      1710      ： 270

下雨的機率則提升為：

1710 / (1710 + 270) = 0.86 = 86%

比起只有烏雲密佈，在螞蟻也出現的情況下，降雨機率又提升了接近 10%。大雄是一個降雨機率不大於 90% 就不帶傘的傢伙，讓我們看看胖虎出沒能不能使他改變心意。

同樣，再次套用定理到上一個（螞蟻的）發生比，則新的（胖虎）事後發生比為：

新雨天數：晴天數 = 原雨天數 * 概度比：晴天數
　　　　　　　　 =  1710  *   3   ： 270
　　　　　　　　 =      5130      ： 270

在轉換成機率之前，我們發現新的雨天數是晴天數的 10 倍以上，因此可以想像新的機率至少是 90% 以上。而實際計算下雨的機率：

5130 / (5130 + 270) = 0.95 = 95%

在觀察到烏雲密佈、螞蟻以及胖虎出沒以後，大雄預估降雨機率上升至 95%，這下不得不帶傘出門了。

動動腦時間¶

到了這邊，我相信你現在應該已經可以在腦中直觀地運用貝氏定理：針對眼前發生的現象，運用過去相關的經驗（計算概度比），來理性地評估某事件可能發生的機率。

事實上在你繼續讀下去之前，我建議先停一停，思考幾個可以實際在生活中運用（或者已經在用）此定理的現象，以幫助你內化（internalize）這些概念。

如果你一時想不到點子，這邊提供幾個例子：

• email 內文裡頭出現「週年慶」時，該郵件為垃圾信的機率
• 新聞內文出現「柯文哲」時，文章主題為政治的機率
• 醫生說你得胰腺癌時，你真的得病的機率
• 玩英雄聯盟時，KDA 超過 4 的對手排位是鑽石以上的機率
• 在東京藥妝店血拼，旁邊講中文的人是台灣人的機率

如果你有其他有趣的例子，歡迎留言跟大家分享。（現在留言不用登入了！）

如同上述，貝氏定理有非常多應用。不過這邊想深入探討第一個 email 的案例：給定一封電子郵件的內文，你要怎麼判斷該信是不是垃圾信件？

從人腦到電腦：讓機器幫我們做判斷¶

你說沒有什麼事情難得了我們人腦。依照過往經驗：

• 垃圾信件裡頭出現「週年慶」一詞的機會是一般信件的 20 倍
• 垃圾信件裡頭出現「折扣」一詞的機會是一般信件的 10 倍

在假設所有信件裡頭一半是垃圾信件（發生比 1：1）的前提下，依照單純貝氏的公式，這封信是垃圾信件的可能性上升 200 倍（20 * 10），我們可以放心把這封信丟入垃圾信分類。

但是沒有人會想要在腦中對每封信做這個運算。人類是懶惰的，能自動化的東西就請電腦幫我們解決就好了。

另外你也不可能記得每一個詞的倍數，實際上也沒有必要。只要讓電腦幫我們記住每個詞分別在垃圾郵件以及一般信件出現的次數，就能計算所有詞彙的概度比（odds）。

等到一封新的信件來以後，找出裡頭的字對應的倍數做相乘以後，電腦就能自動分類郵件了。事實上這就是機器學習中單純貝氏分類器（Naive Bayes Classifier）在做的事情。

讓機器取代人腦自動判斷，有幾個顯而易見的好處：

• 判斷速度倍增
• 記憶能力超強
• （可以把分類郵件空出的時間拿去看貓咪影片）

唷呼！垃圾郵件自動變不見！小鎮村又變得更美好了。

當然你想自己實作單純貝氏分類器的話，Python 可以使用 scikit-learn 來實作。

小心！你的經驗可靠嗎？¶

我們花了很長的篇幅講了幾個貝氏定理/單純貝氏的應用，也看到它既簡單又強大的特性。但在你摩拳擦掌並實際應用此定理的時候，有幾點需要注意：

• 不同現象/事件真的獨立嗎？
• 一開始的猜測以及經驗可靠嗎？

很多現象不一定是完全獨立而是相關的。不過一個常見的解決方法是想辦法增加更多的現象/事件/特徵值（features）來讓做出來的貝氏分類器比較可靠。貝氏定理當然不完美，但正如統計學家喬治·E·P·博克斯所說：

所有模型（models）都是錯的；但有些是有用的。

儘管「獨立」這個假設在某些情況下不合常理，但在如垃圾郵件分類等問題上，貝氏分類器有不錯的表現。而且重點是它實作簡單，可以拿來當作 baseline。

而一開始的猜測跟經驗可不可靠這個問題，英國數學家卡爾·皮爾森，針對貝氏定理則給出一個我很愛的名言：

一個信奉貝氏定理的人常常做這樣的事情：模糊地期待著馬的出現，瞥見驢子的蹤影，強烈地相信他是見到了一匹駝子。

「先入為主」大概是應用貝氏定理最忌諱的點了。下次再套用定理時，記得先思考自己一開始的假設以及經驗是否值得信任或者有什麼盲點。需不需要搜集更多資料來修正一開始的想法。

總結¶

我們在這篇開頭首先用「大雄評估下雨」的例子來直觀地理解貝氏定理背後的精神，接著透過簡單的數學概念、發生比（odds）以及概度比（likelihood ratio）來推出基本的貝氏定理公式。

接著進一步延伸至單純貝氏（naive bayes）的概念，讓機器透過過去累積的資訊，為我們自動分類垃圾郵件。

最後我們提到一些應用貝氏定理需要注意的事情。

即使基本的貝氏定理不難，延伸的領域非常的廣。這篇沒辦法包含所有範圍，但希望透過這篇基礎介紹，能讓讀者能利用貝氏定理的概念，更理性地評估未知並從經驗中學習（或者是建立自己的貝氏分類器）。

另外如果你有其他有趣的例子可以應用在貝氏定理，歡迎留言跟大家分享。（現在留言不用登入了！）