給所有人的深度學習入門：直觀理解神經網路與線性代數

這是篇幫助你直觀理解神經網路的科普文。讀完本文，你將能夠深刻地體會神經網路與線性代數之間的緊密關係，奠定 AI 之旅的基礎。

（小提醒：因本文圖片與動畫皆為黑色背景，強烈推薦用左下按鈕以 Dark Mode 閱讀本文）

這是個對人工智慧（Artificial Intelligence, AI）趨之若鶩的時代。此領域近年的蓬勃發展很大一部份得歸功於深度學習以及神經網路的研究。現行的深度學習框架（framework）也日漸成熟，讓任何人都可以使用 TensorFlow 或 PyTorch 輕鬆建立神經網路，解決各式各樣的問題。

舉例而言，你在 30 秒內就可訓練出一個能夠辨識數字的神經網路：

是的，扣除註解不到 15 行就可以把讀取數據、訓練 model 以及推論全部搞定。這邊秀出程式碼只是想讓你感受一下現在透過框架建立一個神經網路有多麽地「簡單」。事實上，這也是絕大多數線上課程以及教學文章會教你的東西。對此數字辨識應用有興趣的讀者稍後也可自行參考 TensorFlow 的 Colab 筆記本。

我等等要秀給你看的任何一個神經網路都要比這個 model 還簡單個一萬倍（以參數量而言），但觀察並理解這些「簡單」神經網路，將成為你的 AI 旅程中最有趣且實用的經驗之一。

一些有用的背景知識¶

文中有很多動畫帶你直觀理解神經網路（Neural Network, 後與 NN 交替使用）與線性代數（Linear Algebra）之間的緊密關係。以下知識能幫助你更容易地掌握本文內容：

1. 能讀懂文章開頭建立 NN 的 Python 程式碼
2. 了解線上課程都會教的超基本 NN 概念
   • 何謂全連接層（Fully Connected Layer）
   • 常見的 activation functions 如 ReLU
3. 基本的線性代數概念如矩陣相乘、向量空間

別擔心，這些是 nice-to-have。我等等會盡量囉唆點，讓你就算空手而來也能滿載而歸。

另外值得一提的是，本文主要展示已經訓練好的 NN，不會特別說明訓練一個 NN 的細節。

深度學習框架操作容易，但你真的了解神經網路嗎？¶

再次回到文章開頭的 MNIST 例子。

我們剛剛使用 TensorFlow 高層次 API Keras 建立了一個神經網路 model：

# 在 TensorFlow 裡全連接層被稱作 Dense
# 因為這些層之間的神經元「緊密」連接
model = tf.keras.models.Sequential([
  tf.keras.layers.Flatten(input_shape=(28, 28)),
  tf.keras.layers.Dense(128, activation='relu'),
  tf.keras.layers.Dropout(0.2),
  tf.keras.layers.Dense(10, activation='softmax')
])

就跟你在多數教學文章裡頭會看到的一樣，現在要使用深度學習框架建立神經網路十分容易，只要當作疊疊樂一個個 layer 疊上去就好了。下圖則將此 model 用視覺上更容易理解的方式呈現：

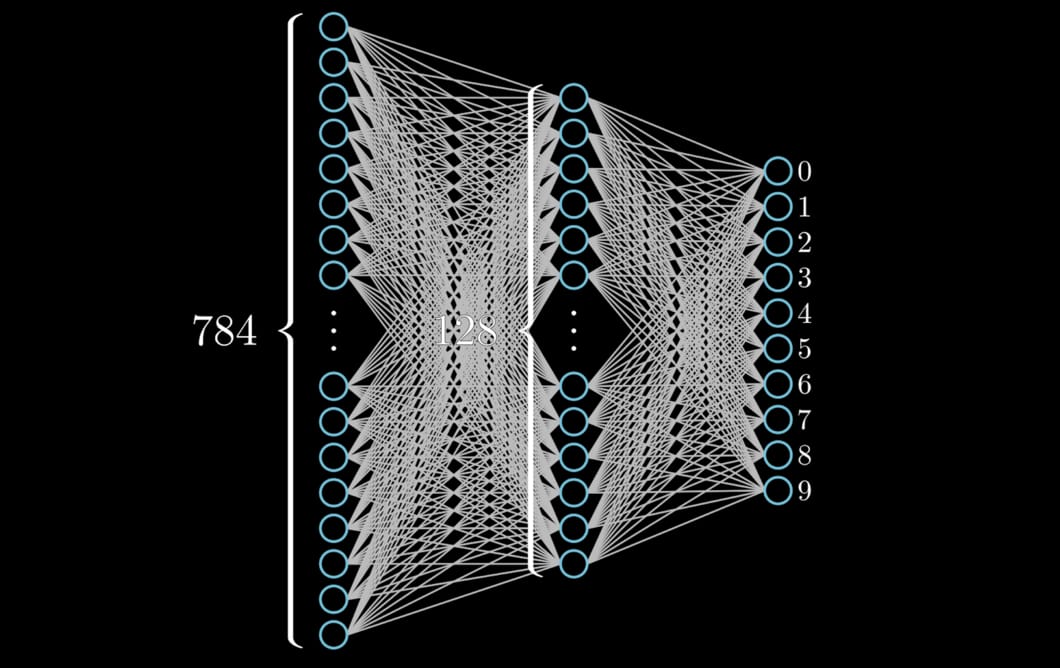
先不看神經網路最左邊的輸入層。右側兩 layers 的每個神經元（neuron）都跟前一層的每個神經元相連，所以被稱之為全連接層（Fully Connected Layer，後簡稱 FC）。而因為相連緊密的特性，TensorFlow 將它們稱作 Dense layer。

我們可以透過 summary 函式輕鬆計算這個神經網路有多少參數：

儘管參數量超過 10 萬，此 model 是個在深度學習領域裡只能被歸類在 Hello World 等級的可憐 NN。畢竟這世界很瘋狂，我們以前討論過的 BERT 以及 GPT-2 都是現在 NLP 界的知名語言模型，而它們可都是擁有上億參數的強大 NN。這些模型的大小可有 model 的 100 倍之大。

但先別管 BERT 或 GPT-2 了，就算是這個 Hello World 等級的 NN，你真的覺得你對它的運作機制有足夠的理解嗎？

講白點，儘管現在路上隨便拉個人都會使用 TensorFlow 或是 PyTorch 來建立神經網路，許多人（包含剛入門的我）對最基本的神經網路的運作方式都沒有足夠直觀的理解。

為了讓你能夠直觀且正確地理解神經網路，我將透過二元分類（Binary Classification）任務說明其與線性代數之間的緊密關係。前言很長，但如果你想要了解神經網路的本質，或是想要為自己之後的 AI 學習之旅打下良好基礎，那我會建議你繼續往下閱讀：）

用二元分類連結神經網路 & 線性代數¶

不只出現在深度學習領域，二元分類是機器學習（Machine Learning）領域裡一個十分基本的任務，其目標是把一個集合裡的所有數據點（data points）依照某種分類規則劃分成兩個族群或類別（classes）。經典的例子有我們之前看過的貓狗圖像辨識。在這篇文章裡，我假設所有數據點最多只有兩個維度（dimensions）。

如果你讀過之前的文章，可能會覺得這假設是在「羞辱」我們。畢竟我們已用過神經網路來：

• 執行假新聞偵測（BERT）
• 生成新金庸小說（GPT-2）
• 把英文翻成中文（Transformer）
• 生成新海誠動畫（CartoonGAN）

這些任務的複雜程度要比二維二元分類多了幾個數量級（當然也非常有趣。你稍後可以點擊相關連結深入了解）。但這篇文章之所以選擇二維二元分類作為目標任務正是因其簡單明暸，我們將能以此窺探神經網路的本質（essence）。

以下是一個包含兩條曲線的資料集：

在此雙曲線資料集裡，兩條曲線分別來自不同類別，各自包含了 100 個數據點 $x$。每個數據點 $x$ 都可以很自然地以二維 $\left (x_{coord}, y_{coord} \right )$ 座標來呈現。右下角也標注了兩曲線所屬類別：黃點的標籤 $y = 0$，藍點則為 $1$。

另外，圖中也描繪了此向量空間中的基底向量：

• x 軸上藍色的 $\vec{i}$
• y 軸上紅色的 $\vec{j}$

等等你會看到，這兩個基底向量（basis vector）能夠幫助我們了解神經網路的運作方式。至於要如何分類這個資料集呢？回想一下之前 AI For Everyone 的重要概念：

目前多數的機器學習以及 AI 應用本質上都是讓電腦學會一個映射函數，幫我們將輸入的數據 x 轉換到理想的輸出 y。
─ Andrew Ng

套用相同概念，要處理這個分類任務，我們要問的問題就變成「給定所有藍點與黃點 $x = \left (x_{coord}, y_{coord} \right )$，我們能不能找出一個 $x$ 的函數 $f(x)$，將這些二維數據 $x$ 完美地轉換到它們各自所屬的一維標籤 $y$ 呢？」

換句話說，我們想要找出一個函數 $f(x)$，使得以下式子成立：

如果我們能找到符合這個條件的 $f(x)$，就能在一瞬間預測出某個數據點 $x_{i}$ 比較可能是哪個類別了。我們有非常多種 model $f(x)$ 的方法，但在線性代數的世界裡，我們可以用矩陣運算的形式來定義一個 $f(x)$：

我希望你至少還記得國中、高中或是大學裡任何一位數學老師的諄諄教誨。

在上面的式子裡：

• $x$ 是一個二維 column vector
• $W$ 是一個 1 × 2 的權重矩陣（weight matrix）
• $b$ 為偏差（bias），是一個純量（scalar）

如果我們先暫時忽略 $b$，事實上 $f(x)$ 對輸入 $x$ 做的轉換跟深度學習領域裡時常會使用到的全連接層（FC）的運算是完全相同的。換句話說，使用一層 FC 的 NN 基本上就是在做矩陣運算（假設激勵函式為線性、偏差為 0）。因此用矩陣運算定義的 $f(x)$ 與神經網路之間有非常美好的對應關係：

沒錯，透過矩陣運算，我們剛剛建立了這世上最簡單的 1-Layer 神經網路！而之所以是 1-Layer，原因在於 NN 的第一層為原始數據（raw data），第二層才是我們新定義的神經網路（一層 FC）。矩陣運算跟 FC 的對應關係家喻戶曉，但這應該是你第一次看到兩者共舞。

從線性代數的角度來看，我們透過矩陣運算將二維的 $x$ 轉換成一維的 $y$；而以神經網路的角度檢視，我們則是將以二維向量表示（represent）的數據點 $x$ 透過與權重 $W$ 進行加權總和後得到新的一維表徵（representation）$y$。這是常有人說神經網路在做表徵學習（Representation Learning）的原因。

另外值得一提的是矩陣 $W$ 裡的每個參數 $w_{mn}$ 實際上就對應到 NN 某一層中第 $n$ 個神經元（neuron）連到其下一層中第 $m$ 個神經元的邊（edge）。別擔心，在本文的最後面還會有動畫幫助你記憶此對應關係。

就跟文章開頭看到的一樣，要使用 TensorFlow 定義這個 1-Layer NN 也十分容易：

扣除偏差後整個神經網路的確只剩 2 個參數。為了讓你加深印象，讓我們將一些數字代入 $W$ 與 $x$：

接著再看一次剛剛的運算過程：

這邊我刻意讓 $x_{1} = x_{2} = 3$。你可以清楚地看到不同大小的 $w_{mn}$ 可以讓不同維度、但相同值的 $x_{n}$ 給與最終輸出 $y_{m}$ 不同程度（權重）的影響力，這也是 $W$ 之所以被稱之為權重（weights）的原因。

你現在知道最基本的矩陣運算、神經網路以及兩者之間的緊密關係了。更美妙的是，如果你已經了解線性代數的本質，就會知道函數 $f(x) = W x + b = y$ 事實定義了兩個簡單轉換來將二維的輸入 $x$ 依序轉換成一維輸出 $y$：

1. 線性轉換：$W$
2. 位移：$b$

你多年前可能也已看過線性轉換（linear transformation, or linear map）的正式數學定義：

這是所有線性轉換都具備的可加性（additivity）與齊次性質（homogeneity）。不過別擔心，在本文裡你不需了解這些定義也能直觀地理解線性轉換。用比較不嚴謹的說法，線性轉換會對其作用的向量空間（vector space）做旋轉、伸縮等「簡單」轉換。

要直觀瞭解這個概念，讓我們再次將幾個數字代入 $f(x)$ 的參數裡頭：

這次假設 $w_{11} = w_{12} = 1, b = -2$。另外別忘了我們剛學的，這個函數 $f(x)$ 可以被表示成到一個特定的 1-Layer NN。我們可以觀察這個 NN（即 $f(x)$）如何轉換二維空間裡頭的 $x$：

這個 NN 做的轉換十分簡單，但是隱含了不少重要概念。

首先，以神經網路的角度解讀 $f(x)$ 的話，此二維向量空間裡頭的任一數據點 $ x = \left (x_{coord}, y_{coord} \right )$ 都對應到左上 NN 第一層（輸入層）中的 2 個神經元。權重 $W$ 則以邊的方式呈現，負責將第一層中 2 個神經元的值依照不同比重送去啟動（activate）下一層的神經元。啟動下層神經元後，NN 只要再將一個偏差值 $b$ 加到該神經元即完成此 layer 的轉換。

以線性代數的視角檢視 $f(x)$ 的話，裡頭的矩陣 $W$ 則定義了一個線性轉換。此轉換說明了原向量空間 $V_{original}$ 裡的 2 個基底向量 $\vec{i}$、$\vec{j}$ 在轉換後的一維空間 $V_{transformed}$ 中的目標位置。$w_{11} = 1$ 讓原 x 軸上的 $\vec{i}$ 保持在「原位」；$w_{12} = 1$ 則將 $\vec{j}$ 放到 $V_{transformed}$裡與 $\vec{i}$ 一樣的位置。

此例中 $V_{transformed}$ 是一個跟 x 軸重疊的一維數線（Number line），你在動畫最後面也可以看到 $\vec{i}$ 跟 $\vec{j}$ 在此數線上的相同位置。為了讓轉換過後的 $\vec{j}$ 能在指定的位置，y 軸順時針旋轉並轉換到了 $V_{transformed}$ 之上。你也能看到原二維空間裡頭的每個數據點 $x$ 都跟著 $\vec{j}$ 一起被轉換成該數線上的一個值，而不再是二維座標。透過 $W$ 被轉換到一維空間以後，該數線上的每個數據點只要再被加上偏差 $b$ 就完成兩步驟的轉換。

我幫你用兩種角度檢視 $f(x)$，但這邊最重要的啟示是：

你可以用神經網路或是線性代數的角度來解讀 $f(x)$ 的作用，但兩者殊途同歸：它們實際上都是利用 $f(x)$ 將原始數據 $x$ 進行一系列幾何轉換後輸出理想的 $y$。

這也是為何我們之前說神經網路本質上是一個映射函數的原因。

怎樣的神經網路才是好的分類器？¶

我們剛剛看到，1-Layer NN 可以透過一個 FC（線性轉換 $W$ + 位移 $b$）將二維輸入 $x$ 轉換成一維輸出 $y$。不過由於我們剛剛是隨意設定參數 $W$ 及 $b$，如果以分類器（classifier）的標準去評價該 NN 的話，其表現實在是令人不敢恭維。

讓我們快速回顧一下剛剛的 NN 做了怎樣的轉換，並計算分類準確率：

我盡量讓所有動畫 speak for themselves，但希望你不介意我再嘮叨一下。

我們一樣透過 $f(x)$ 將兩組分別以黃色及藍色表示的二維數據點 $x$ 轉成一維的 $y$。轉換之後我們能找出一個 $y$ 值（此例中 $y = 1$），畫條垂直線將兩組輸出 $y$ 分開。這條分類界線（classification boundary）能使我們分對最多的 $x$。

我們可以用此分界線定出一個分類規則：任何數據點 $x$ 只要它的 $f(x) = y$ 在這條線的左邊，我們就預測其來自黃色曲線，反之則為藍色曲線。很明顯的，黃色在此界線的左側則是因其標籤數值（label）比藍線小。

溫馨提醒，這是我們剛剛用來轉換 $x$ 的神經網路 $f(x)$：

將 $W$ 設為 $[1, 1]$、$b$ 設定為 $-2$ 以後，$f(x)$ 函數對輸入 $x$ 做的轉換不至於錯得離譜，但也就只能把觀測到的 200 個數據點 $x$ 裡頭的 68 個點正確分類，其準確率（accuracy）只有 66%。很明顯的，要透過 $f(x)$ 來解決當前的二元分類任務，我們要問的問題變成：

這組參數的選擇是最佳解嗎？能不能找到一組最好的參數 $W$ 與 $b$，使得 $f(x)$ 最後的分類準確率最大？

答案當然是肯定的 Yes，只要適當地運用以下數學概念與技巧就能做到：

• 微積分（Calculus）
• 梯度下降（Gradient Descent）
• 反向傳播演算法（Back Propagation）

這也是深度學習核心之一的學習過程。在此例的 $f(x)$ 裡頭，其參數 $W$ 與 $b$ 的實際數值會在模型的訓練過程中不斷地被修正以提升分類準確率，所以一般會被稱作可訓練的參數 $\theta$。事實上，我們前面定義 $f(x)$ 時，並不只是定義一個特定的函數，而是一整個函數空間 $f_{\theta}(x)$。此空間裡頭的每個函數雖然架構上都是先對 $x$ 做線性轉換再進行位移，但因其參數值 $\theta$ 皆有所不同，實際上做的轉換也就有所差異。這也就意味著：

我們可以透過矩陣運算的形式定義一個神經網路架構 $f_{\theta}(x)$，再透過微積分與反向傳播等方式，求得此架構裡能最能有效解決任務的參數 $\theta$。

這是為何有人會跟你說要真的學好深度學習，線性代數以及微積分很重要的原因。前者讓你定義出一個具有解決複雜問題「潛力」的數據轉換架構（神經網路），後者則讓你實際找出每個轉換步驟所需的細節（參數權重）。當然，就算你完全不懂後者，深度學習框架也能幫你搞定一切：

# 文章開頭的 MNIST 範例程式碼片段
# 定義一個能夠解決問題的模型架構
model = ...

# 設置學習實際參數所需的東西：損失函數、optimizer
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# 訓練模型，取得最好的參數 theta
model.fit(x_train, y_train, epochs=5)

# 打完收工

不幸的是，深度學習框架的方便也成為很多人不明就裡的原因之一。

如本文開頭所述，我的目標是讓你可以透過線性代數來直觀地了解已訓練好的 NN 如何轉換數據並達成任務目標。因此底下展示的都是我先幫你訓練好的 NN（即我們已經知道最好的 $\theta$ 為何）。你等等可以參考我在文後附上的連結，深入了解如何實際訓練一個 NN，找出一組好的參數 $\theta$。

事不宜遲，讓我們馬上看看一個訓練好的 1-Layer NN 能把這個二元分類任務做到多好：

簡單而完美。事實證明，只要使用適合的參數 $\theta$，用矩陣形式定義的這個 1-Layer NN 能夠完美地將這兩條曲線分開。另外，如果你再稍微仔細觀察最初的雙曲線並結合前面談到的矩陣概念，就會發現 $W$ 這個線性轉換是非常有意思的：

你可以用底下動畫再次觀察轉換前的二維向量空間。

你會發現黃藍雙曲線本身雖然看似複雜，其實只要用一條幾乎跟 x 軸重疊的水平線就能將兩者切開。這也就意味著二維數據點 $x = \left (x_{coord}, y_{coord} \right )$ 裡頭的第一個維度 $x_{coord}$ 的值幾乎不會影響分類兩曲線的決策。此 NN 學會將 $w_{11}$ 設成一個很小的值 $0.01$，讓原空間中 x 軸上的值都壓縮到幾乎等於 0。檢視動畫左上的 NN 示意圖，你會發現代表 $w_{11}$ 的第一條邊幾乎沒有將輸入層中第一個神經元的值 $x_{coord}$ 傳給輸出神經元。這也就代表 $x_{coord}$ 不太影響最後的 $y$ 值。

而因為一個數據點的第二個維度 $y_{coord}$ 才是用來判斷其所屬類別的重要信號（$y_{coord}$ 越大，藍線機率越大），且理想上轉換後的藍點標籤 $y$ 要大於黃點的 $y$，因此這個 NN 將 $w_{12}$ 設為一個相對 $w_{11}$ 大的正值，將原空間 $V_{original}$ 的 y 軸順時針旋轉，讓所有藍點的 $y$ 皆大於黃點的 $y$。很有意思，對吧？你可以把矩陣 $W$ 裡頭的值換掉，並測試看看自己是否能在腦海中想像其對應的線性轉換過程。

由淺入深：解決看似不可能的分類任務¶

如果有反覆觀看前面動畫並停下來動腦思考，我相信你現在已經能夠直觀地理解並想像一個 1-Layer NN 是怎麼解決二元分類問題的。這是一個很不錯的開始。在這小節，我想提升分類任務的難度，讓你再多點對神經網路的直觀感受。

比方說我們可以將剛剛 1-Layer NN 完美分類的兩條曲線拉「近」點：

很明顯地，你現在再也無法找到一條平行線來將兩者切開了。相較於我們前面看過的簡單雙曲線，現在這兩條曲線靠得更近，也讓神經網路更難將它們切開了。讓我把這個新的資料集稱作困難雙曲線。

因為我們前面看過的 1-Layer NN 只透過 FC 做一組簡單的線性轉換與位移，我並不認為它能在困難雙曲線上得到多好的結果。不過眼見為憑，還是讓我們看一下 1-Layer NN 在困難雙曲線上的表現：

不需特別計算準確率，你一眼就能看出 1-layer NN 在這資料集上表現地實在是力不從心。兩條曲線在被轉換之後仍然有非常多的重疊部分。換句話說，此 NN 做的（線性）轉換並無法將兩個不同類別的數據點 $x$ 完全分開。

以線性代數的角度來看，這個 NN 就是透過矩陣 $W$ 對整個二維空間做一致的旋轉與伸縮，無法針對性地將兩條緊靠的雙曲線在空間中拉扯開來。不過別擔心，深度學習領域裡的人最愛玩疊疊樂了。讓我們多疊一層全連接層（FC），看看新的 2-Layers NN 如何處理這個問題：

這個 2-Layers NN 的表現如你預期嗎？還是讓你失望了？在找戰犯之前，讓我先說明基本概念。

雖然這是本文第一次展示 2-Layers NN，動畫應該已經把所有東西都交代得很清楚了。一個 FC 就對應到一組矩陣 $W$ 以及偏差 $b$，因此一個有兩層 FCs 的神經網路 $g(x)$ 實際上就是對 $x$ 做兩次矩陣運算（與加上偏差）：

這邊 $W_{i}$ 與 $b_{i}$ 分別代表第 $i$ 個 FC 的權重矩陣與偏差。

2-Layers NN 裡頭的矩陣 $W_{1}$ 跟 1-Layer NN 裡頭的矩陣 $W$ 都代表著第一個 FC 做的線性轉換。但跟 1-Layer NN 不同的地方在於，$W_{1}$ 並不是直接把原始數據點 $x$ 轉換成一維的 $y$，而是先將 $x$ 轉到另個形式的二維表徵 $h$，接著再讓下一層 FC 將 $h$ 轉換至一維的 $y$。像是這種只存在輸入與輸出之間的表徵一般被稱作隱藏表徵（hidden representation），而生成這些表徵的 FC 層自然就被稱作隱藏層（hidden layer）。

而建構這種數據轉換架構的背後精神就是表徵學習（Representation Learning）：

透過對輸入 $x$ 做一連串簡單的幾何轉換，將此原始表徵 $x$ 逐漸轉換成能夠用來解決我們問題的隱藏表徵 $h$，最後輸出成目標結果 $y$。

雖然這邊的 2-Layers NN 表現不佳，但這概念可是你在剛接觸深度學習時值得畫上三顆星的重點之一。

回到剛剛的 2 × 2 的 $W_{1}$ 矩陣。跟之前 1 × 2 矩陣一樣，這次讓我們看看 $W_{1}$ 跟 FC 之間的關係：

你可能注意到矩陣 $W_{1}$ 裡頭每一行（column）顏色皆不相同。

矩陣 $W_{1}$ 定義了一個線性轉換，而裡頭的每個 column 則定義了原空間 $V_{original}$ 中的各個基底向量在新空間 $V_{transformed}$ 中的位置。而以神經網路的角度來看，矩陣 $W_{1}$ 中的每一行則對應到某個神經元連到下一層所有神經元的權重值。

另外值得一提的是，FC 跟矩陣的緊密關係事實上也部分解釋了為何神經網路常以一層層（Layered）形式出現的原因。雖然這邊的 NN 只有兩層，在深度學習領域裡我們時常會想對原始數據 $x$ 進行幾十、幾百次的轉換，而由一連串矩陣組成的運算非常容易平行化，因此在建立深度神經網路（Deep Neural Network）時，疊很多以矩陣運算為基礎的 Layers 是一個非常主流的做法。

至於為何剛剛的 2-Layers NN 無法解決困難雙曲線？

在了解矩陣運算以及線性轉換以後，一切都變得很容易解釋。結合前面所學：

• 一層 FC 對應到一矩陣運算（加偏差）
• 一個權重矩陣對應到一個線性轉換
• 一個線性轉換會對作用空間做旋轉伸縮

就可以得知我們的 2-Layers NN $g(x)$ 事實上就是對原空間裡頭的數據點 $x$ 做連續兩次的旋轉與伸縮（當然，動畫已經告訴我們這件事情了）。很直觀地，不管神經網路做幾次這樣的轉換，最後的效果都可以被單一線性轉換取代。換句話說，對困難雙曲線連續做好幾次線性轉換是不會得到比單一線性轉換更好的結果的。你可以拉回去看看 2-Layers NN 如何「瞎忙」。

解法也很直覺。我們可以找一個非線性函數如 ReLU 當作 FC 層的激勵函數（activation function），讓 FC 層跟其他層之間有非線性的轉換，讓神經網路掌握超越線性轉換的能力。

以下就是將 ReLU 加入 2-Layers NN 並解決困難雙曲線分類的過程：

這個轉換過程超美的，不是嗎？這個神經網路只有 9 個參數，卻是我看過最美麗的神經網路之一。

透過線性轉換與非線性轉換的交替使用，升級後的 2-Layers NN $h(x)$ 成功地將困難雙曲線任務解開，辦到前一代 $g(x)$ 做不到的事情，而兩者只差在一個 ReLU 函數：

再次提醒，激勵函數 $a(z) = relu(z)$ 一般是被各別套用到在計算完 $W(x) + b = z$ 的神經元之上，不需做矩陣運算，因此幾乎沒有計算成本（好啦，還是要看是哪個函數）。在深度學習領域裡，使用非線性函數來提升神經網路的處理能力是件稀鬆平常的事。除了常用的 ReLU 之外，其他知名的函數包含了 Sigmoid、Tanh 以及 Leaky ReLU 等等。

到此為止，你也已經了解非線性函數之於神經網路的重要性了。我們的旅程也將進入尾聲。

結語：往下一站出發¶

呼！不知不覺就到了這趟旅程的終點了！結束地真快，你說是吧？

就算你一開始什麼都不懂，在閱讀本文以後你應該已經能夠：

1. 了解最基本的矩陣運算、神經網路以及兩者之間的緊密關係
2. 想像線性轉換如何對向量空間做旋轉、伸縮等基本轉換
3. 理解並想像一個 1-Layer NN 怎麼解決二元分類問題
4. 了解如何透過矩陣運算的形式定義一個神經網路架構 𝑓𝜃(𝑥)
5. 使用神經網路或是線性代數的角度來解讀 𝑓𝜃(𝑥) 的作用
6. 明白神經網路就是將原始數據 𝑥 進行一系列幾何轉換後輸出理想的 𝑦 的映射函數
7. 瞭解如何透過非線性的轉換，讓神經網路掌握更進階的能力
8. 自由地連結矩陣運算以及神經網路的概念並在兩者之間切換

沒錯，你可能會驚訝於自己學了那麼多。更美妙的是透過大量動畫，很多概念應該都已經深深地烙印在你的腦海中，你甚至不需要背什麼東西。在這個 AI Hype 時代，我們沒有談最新的 AI 論文，也沒有用深度學習框架做什麼酷炫的應用，但我相信這樣的文章才是大部分人以及生活在 AI 時代的下一代所需要的。

如果你想要學習更多線性代數以及微積分的相關知識，強力推薦 3Blue1Brown 的 Youtube 頻道 ，本文所有動畫也都是用該頻道作者 Grant Sanderson 開源的 Manim 製作的。另外如果你想要深入了解深度學習，由淺入深的深度學習資源整理是一個好的開始。

如果你已經有點 Python 基礎，想要看深度學習還能拿來做些什麼，可以參考之前的文章：

• 寫給所有人的自然語言處理與深度學習入門指南
• AI 如何找出你的喵：直觀理解卷積神經網路。
• 進擊的 BERT：NLP 界的巨人之力與遷移學習
• 直觀理解 GPT-2 語言模型並生成金庸武俠小說
• 淺談神經機器翻譯 & 用 Transformer 與 TensorFlow 2 英翻中
• 用 CartoonGAN 及 TensorFlow 2 生成新海誠與宮崎駿動畫

底下是我為你做的最後一個動畫。你可以用它來測試自己在本文的所學，並熟悉矩陣與神經網路之間的關係。注意矩陣行與列中的參數 $w_{mn}$ 是怎麼對應到神經網路的邊（edge）的。

在這個 AI 新聞滿天飛的時代，我希望這篇入門文章可以幫助更多人直觀地理解其背後的核心動力：神經網路並開始自己的 AI 之旅。如果這篇文章有幫助到你，希望你能發揮舉手之勞，幫忙分享本文，以讓更多、更多的人可以加入這個行列。

也希望你喜歡這首神經網路與線性代數的雙重奏，我們下次見。